요즘 습관적으로 로또복권을 매주 한 줄씩 구매하게 되는데 갑자기 문뜩 궁금해졌다. 로또복권에 100% 당첨되려면 얼마나 투자를 해야 하며 그것이 현실적으로 가능한지 만약 가능하다면 투자금액 대비 어느 정도 수익을 볼 것이며, 불가능하다면 몇 줄을 구매해야 가성비인지. 직접 확인을 위해 계산해보기로 했다.
과연 로또복권은 수익률이 얼마나 될까?
1. 시장 규모

로또복권 시장 규모는 2007년 이후 꾸준히 상승세이며 2021년 12월 11일 기준 복권 판매대금이 4.9조로 2021년 말까지 5조를 넘어설 것으로 예상된다.
로또는 기획재정부 산하 복권위원회가 지정한 수탁사업자인 동행복권에서 발행하고 있으며 복권 판매 대금의 약 50%를 당첨금액으로 지급하고 있다.
시장규모로 보았을 때 2021년 기준 약 2.46조를 당첨금액으로 지급하였고 매 회차마다 491.84억씩 지급한 것으로 확인된다.
2002년 로또산업이 처음 출범했을 땐 한 게임당 2,000원이었고 당첨금도 엄청났지만 얼마 뒤 한 게임당 1,000원으로 인하되면서 기대수익이 줄어들자 로또 판매량도 같이 줄었다. 그러다 2007년부터 다양한 이슈들과 함께 경기불황이 장기화되면서 로또 판매량은 해마다 꾸준히 증가하였다.
코로나19, 금리인상, 인플레이션 등 앞으로도 불경기가 지속된다면 한방을 노리는 사람들도 더 많아질 것으로 예상된다.
2. 당첨 확률
복권에 100% 당첨이 되기 위해서는 로또번호가 가지는 모든 경우의 수를 알아야 한다.
로또복권은 1~45번 중 6개 번호를 비 복원 추출하여 추첨번호와 일치하면 1등 당첨금을 받을 수 있다.
45번 중 6개를 뽑았을 때 나올 수 있는 경우의 수를 수학적으로 풀이해보면
45C6 = 45!/(6!*39!)라는 식이 나온다.
위 식을 파이썬 재귀함수로 계산을 해보면
def factorial(n):
if n < 1:
return 1
else:
return n * factorial(n - 1)
def nCr(n, r):
return int(factorial(n)/(factorial(r)*factorial(n-r)))
print(nCr(45,6))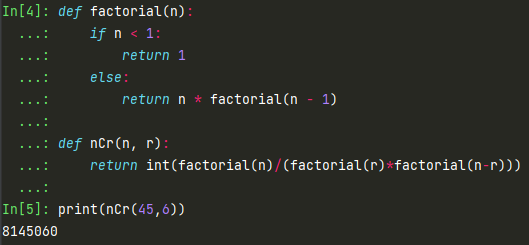
8,145,060이라는 숫자가 나온다. 즉, 45개 중 6개를 중복이 안되게 뽑는다면 8,145,060가지 경우의 수가 나오게 된다.
이는 로또 1등 당첨 확률이 1/8,145,060이며 확률로 0.00001%라는 것을 의미한다.
공식에 나오는 !는 팩토리얼인데 팩토리얼은 1부터 어떤 양의 정수 n까지 곱한 것을 말한다.
예를 들어 6!이면 6*5*4*3*2*1이다.
재귀함수는 파이썬 알고리즘 중 하나로 함수 내 함수를 호출하여 반복적으로 동작하게 하는 알고리즘이다. 재귀함수는 작업이 종료될 때까지 계속 호출되는 함수이기 때문에 함수 정의시 종료 조건을 꼭 넣어주어야 한다. 종료 조건을 넣지 않을 경우 무한루프에 빠지게 된다.
재귀함수 외에도 for문이나 while문 등 여러 함수를 조합하여 팩토리얼을 구할 수 있지만 오늘은 재귀함수를 사용했다.
3. 수익성 분석
로또는 전체 복권판매 대금의 약 50%를 당첨금액으로 배분하고 있으며 1~45번 중 6개 번호를 비복원 추출하여 추첨번호와 일치하면 당첨금액을 수령할 수 있다. 전체 당첨금액 중 4등과 5등 당첨금을 제외하고 1등 75%, 2등 12.5%, 3등 12.5%씩 분배된다.
앞서 확인한 로또 수령금액은 회차당 491.84억이고 모든 경우의 수를 다 찍는다고 가정하면 1등부터 5등까지 동시 당첨될 수 있다.
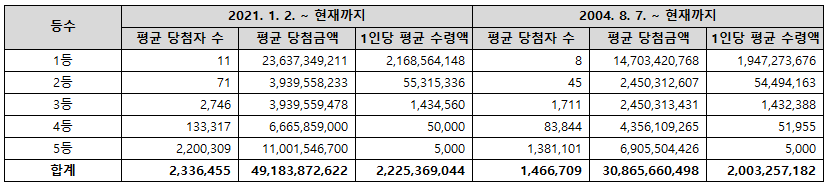
당첨금을 모두 수령하면 좋겠지만 동시 당첨자가 존재하기 때문에 불가능하다. 동시 당첨자를 고려하여 1등부터 5등까지 모두 당첨될 경우 평균적으로 22.25억 정도 수령할 것으로 예상된다.

로또복권에 모두 당첨되어 22.25억을 수령하였다고 가정한다면 3억 이하 분에 대한 세금 0.66억, 3억 초과 분에 대한 세금 6.35억 총 7.01억을 세금으로 지불해야 하며 세금공제 후 실수령액은 15.24억이다.
1등부터 5등까지 모두 100% 당첨이 되려면 앞서 확인한 경우의 수(8,145,060)만큼 로또를 구매해야 하며 계산해보면
8,145,060 * 1,000 = 8,145,060,000라는 금액이 나온다.
81억이 넘는 금액을 투자하여 받을 수 있을 것으로 예상되는 기대수익은 15.24억이다. 투자금액 대비 절반도 미치지 않은 금액이다.
만약 1~5등 중 1등만 동시 당첨자가 없다고 가정하면 예상 당첨금은 236.94억으로 여기서 세금 77.86억을 공제한다면 예상 실수령액은 159.08억이다. 1등 동시 당첨자만 없다면 투자금액 대비 2배에 가까운 수익을 볼 수 있지만 로또사업이 시작되고 지금까지 당첨자가 0명일 때는 고작 14번뿐이었다. 전체 993회 차 대비 1.41% 수준이다.
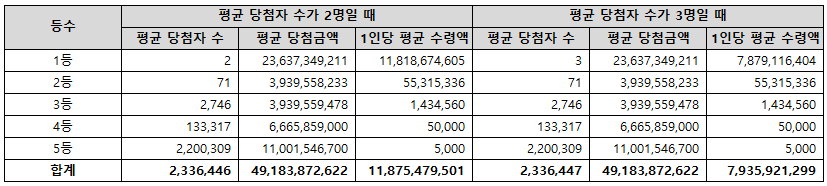
투자금액 대비 손익분기점을 넘기려면 1등 동시 당첨자가 2명을 넘지 말아야 한다. 로또 전체 회차 중 당첨자가 0~1명일 때는 총 42번이다. 전체 993회차 대비 4.23%이다.
마무리
로또복권에 100% 당첨이 되려면 약 81.45억이 필요하며 투자한 금액이상 수익을 볼 확률은 4.23%이다.
따라서 투자매력은 없는 것으로 확인되며 로또 1등에 당첨될 확률은 0.00001%, 중복이 안되게끔 5번을 찍으면 0.00006%로 1줄을 구매하던 5줄을 구매하던 1등에 당첨될 확률은 극히 희박하다.
def factorial(n):
if n < 1:
return 1
else:
return n * factorial(n - 1)
def nCr(n, r):
return int(factorial(n)/(factorial(r)*factorial(n-r)))
print('1등: {:.6f}%'.format((1/nCr(45,6))*100))
print('2등: {:.6f}%'.format(nCr(6,5)/nCr(45,6)*100))
print('3등: {:.6f}%'.format((nCr(6,5)*nCr(39,1))/nCr(45,6)*100))
print('4등: {:.6f}%'.format((nCr(6,4)*nCr(39,2))/nCr(45,6)*100))
print('5등: {:.6f}%'.format((nCr(6,3)*nCr(39,3))/nCr(45,6)*100))
로또를 구매하지 않으면 당첨될 확률은 0%다. 하지만 1줄이라도 구매한다면 1등 당첨될 확률은 희박하지만 상대적으로 높은 확률로 2~5등에 당첨될 수 있으며 당첨이 안되더라도 추첨 전까지 기대감을 준다.
추첨은 매주 토요일 20시 45분에 진행하며 다음날 6시부터 다음 회차 복권을 판매하기 때문에 일요일날 구매하면 기대감을 가장 오래 느낄 수 있다.
결론: ① 세상은 호락호락하지 않다. ② 가성비 = 일요일 로또 1줄
'국내외 경제소식' 카테고리의 다른 글
| 금값이 오르는 진짜 이유와 비트코인 비교 분석 (1) | 2025.06.02 |
|---|---|
| 전쟁과 경제: 내 자산은 안전할까? 투자자 관점에서 살펴보기 (1) | 2025.05.30 |
| 미국 기준금리 변화, 한국 경제에 어떤 영향을 줄까? (0) | 2025.05.22 |
| 미국 관세폭탄, 한국경제는 괜찮을까? (1) | 2025.05.12 |



